1. 개요
인공신경망(artifical neural networks)으로 불리는 신경망(neural networks) 모형은 분류와 예측을 위해 사용되는 모델이다. 신경망은 인간의 뇌 속 뉴런들이 서로 상호 작용을 하고 경험을 통하여 배우는 생물학적 활동을 모델화한 것이다. 신경망은 어린아이가 태어나면서부터 배우는 방식을 흉내 낸 것이라고 생각하면 쉽다. 신경망의 학습 및 기억 특성들은 인간의 학습과 기억의 특성을 닮았고, 특정 사건으로부터 일반화하는 능력 또한 가지고 있다.
신경망의 가장 큰 장점은 높은 예측 정확도에 있다. 신경망의 구조는 다른 분류모델에서는 불가능한 입력변수와 출력변수 사이의 매우 복잡한 관계를 파악한다.
2. 신경망모델의 개념 및 구조
신경망의 기본 아이디어는 입력변수들 사이 또는 입력변수와 출력변수 사이의 복잡한 관계를 파악할 수 있는 매우 유연한 방법으로 입력정보를 결합하는 것이다. 선형 회귀모형에서 입력 변수와 출력 변수 사이의 관계는 선형으로 가정되지만 대다수의 경우에는 변수들 간의 정확한 관계는 훨씬 더 복잡하거나 일반적으로 알려져 있지 않다.
신경망에서는 사용자가 모델의 정확한 조건을 상세하게 지정할 필요가 없다. 그 대신 신경망은 이러한 관계를 데이터로부터 직접 학습을 통하여 찾으려고 시도한다.
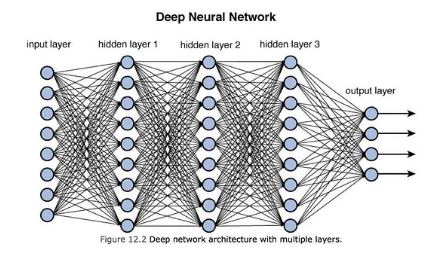
그동안 많은 연구들이 수많은 다른 신경망 구조를 연구했지만, 신경망을 이용한 데이터마이닝의 가장 성공적인 아이디어는 다중 전방향 신경망(multi-layer feedforward networks)이다. 단순히 입력값을 받아들이는 노드로 구성된 입력층과 이전 층으로부터 입력정보를 받아 전방향으로 학습하는 층(보통 이를 은닉층이라 한다.), 마지막 출력을 담당하는 출력층이 있다.

3. 신경망 학습
1) 노드값 계산
신경망의 3가지 유형(입력층, 은닉층, 출력층)의 층에 대해서는 노드의 입력과 출력으로 나누어 설명할 수 있다. 각 층의 주요 차이점은 노드의 입력에서 출력까지의 연결되는 함수에 의해 결정된다.
입력노드는 예측변수의 값을 입력하는 역할을 한다. 입력노드의 출력은 입력값과 같은 역할이다. 각 입력 노드는 은닉층의 노드로 전달된다.
은닉층 노드는 입력층의 출력값을 은닉층의 입력값으로 사용한다. 은닉층의 출력값을 계산하기 위해서는, 입력변수값의 가중합을 계산하고 이 값을 전이함수에 적용한다.
출력층은 바로 이전의 은닉층으로부터 입력값을 얻는다. 출력층의 출력값을 얻기 위해서는 은닉층과 같이 전이함수가 적용된다.
2) 데이터 전처리
신경망은 입력변수와 출력변수가 [0, 1] 사이에 있을 때 최대의 성과를 낸다. 이러한 이유로 인해 모든 변수들은 신경망에 입력하기 이전에 [0, 1]로 변화되어야 한다.
신경망의 성과를 개선시키는 방법 중 하나로 한쪽으로 매우 기울어진 데이터 분포를 정상적인 분포(예: 정규분포 등)가 되도록 변환시키는 것이다. 이때 변수를 로그변환 시킬 경우 이 변숫값은 대체로 대층적인 분포로 바뀌게 된다.
3) 모델 학습
모델을 학습시키는 것은 가중치를 추청하여 최적의 예측값을 찾는 것을 의미한다. 하나의 관찰치를 이용하여 신경망 출력값을 계산하는 과정은 학습용 집합에 있는 모든 관찰치를 대상으로 반복한다. 각 관찰치별로 신경망모델은 예측값을 계산하고, 이 예측값을 실제값과 비교한다. (오차 계산). 예측값과 실제값의 오차를 이용하여 반복적으로 추정가충치를 갱신시킨다.
* 오차 역전파
역전파 알고리즘은(back propagation algorithms)은 가중치를 갱신하기 위해 모델의 오차를 이용하는 방법이다. 이름이 의미하듯이 출력층에서 이전 은닉층으로 이어지는 역방향으로 오차를 계산한다. 여기서 학습률(learning rate)이라는 파라미터가 있는데, 일반적으로 0과 1 사이 범위에서 상수로 존재하고, 한번 학습이 일어날 때마다 학습률을 이용하여 가중치의 변동량을 제어하게 된다. 가중치 감소 (weight decay) 파라미터는 가중치 조정 시에 가중치를 감소시키는 파라미터이다. 학습용 데이터 집합에서 신경망의 과적합 현상을 방지하기 위해 사용한다.
가중치를 갱신하는 방법은 사례별 갱신과 일괄갱신이 있다 사례별 갱신의 경우 각 관찰치가 신경망에 적용될 때마다 가중치가 갱신된다. 이를 가중치 조정시도라 한다.
관찰치를 통해서 학습시킨 후 기존 가중치가 새로운 가중치로 갱신되고, 그 다음 관찰치를 통해서 다시 가중치가 새롭게 갱신되며 이러한 과정은 모든 관찰치가 한 번씩 적용될 때까지 계속된다. 그리고 이러한 신경망 학습은 전체 관찰치를 몇 번 학습하게 된다. 이를 epoch이라 한다.
가중치 갱신은 어느 시점에서 종료 되어야 하는가? 이에 대한 일반적인 고려사항은 다음과 같다.
- 새로운 가중치가 이전에 조정된 가중치에 비해 단조 증감할 때
- 오분류율이 사전에 정한 기준값에 도달할 때
- 가중치 조정이 미리 정해진 학습횟수까지 이루어졌을 때
4) 출력값을 이용한 예측 및 분류
수치형 반응변수를 예측하기 위해 신경망을 사용할 때에는 최종 출력값을 반응변수의 원래 측정 단위로 되돌리기 위한 척도 수정이 필요하다. 측 신경망에서는 일반적으로 [0, 1] 사이 구간의 척도로 출력하기 때문에 이를 원래의 사용 목적에 맞도록 변경하여야 한다.
m개의 집단을 갖는 분류문제에 신경망을 사용할 경우는 m개의 출력노드에서 각각 출력값을 얻게 된다. 이때 m개의 출력값을 분류규칙을 변환시키는 방법은 가장 큰 출력값을 갖는 노드를 신경망의 분류값으로 결정하는 것이다. 보통 확률로 정의하는데 m개의 출력 노드의 확률값의 합을 1로 두고 각 출력의 확률을 계산하게 된다.
4. 사용자 입력 요구사항
역전파 알고리즘을 이용한 신경망모델을 적용할 때에는 많은 시간이 필요하다. 그리고 신경망의 구조를 선택하는 일이 더욱 어렵다. 보통은 과거의 경험을 이용하여 가능성이 높은 구조를 선택하고 여러 번의 시행착오를 거쳐 최종 구조를 선택한다.





댓글